等腰三角形的判定与性质

等腰三角形，作为一种特殊的三角形，拥有许多独特的性质。如何确定一个三角形是等腰的？又该如何运用它的性质？本文将详细为您解答。

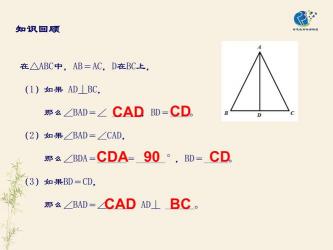
判定方法：

当三角形中某一角的角平分线与它所对的高完全重合时，这个三角形便是等腰的。

若三角形的一边上的中线与这条边上的高完全重合，该三角形也是等腰的。

主要性质：

两底角相等：在等腰三角形中，两个底角总是拥有相同的度数，此特性可以简洁地表示为“等边对等角”。

三线合一：等腰三角形的顶角平分线、底边上的中线以及底边上的高都是同一条线。这可以简称为“等腰三角形三线合一”。

角的平分线与边的关系：在等腰三角形中，两底角的平分线长度相等，同时两条腰上的中线和两条腰上的高也都相等。

底边的垂直平分线与腰的关系：从等腰三角形的底边上的垂直平分线出发，到两条腰的距离是相等的。

高与底边的夹角关系：等腰三角形的一腰上的高与底边所形成的夹角，恰好是顶角的一半。

底边上任意一点与两腰的关系：在等腰三角形的底边上，任选一点，该点到两条腰的距离之和恒等于一腰上的高。这一特性可以通过等面积法来证明。

轴对称性：通常的等腰三角形具有轴对称性，且只有一条对称轴，即顶角平分线所在的直线。但特殊的等腰三角形——等边三角形具有三条对称轴，分别是每个角的角平分线、三条中线以及三条高所在的直线。

腰与高的关系及其与底边的勾股关系：在等腰三角形中，腰的长度总是大于高；而腰的平方等于高的平方加上底边一半的平方，这实际上也是勾股定理的一种应用。

通过本文，我们深入了解了等腰三角形的判定方法以及它所具备的各种性质。这些知识在数学证明和解决实际问题中都将是您有力的工具。