证明：设三角形为ABC，E、F是AB、AC的中点，EC、FB交于G。由平行线分线段成比例定理，可得AH=HF=1/2AF，进一步得到HF:CF=1/2，以及EG:CG=HF:CF=1/2，因此EG=1/2CG。

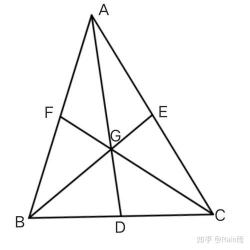
重心和三角形3个顶点组成的3个三角形面积相等。

证明方法：在△ABC内，三边为a、b、c，点O是该三角形的重心，AOA'、BOB'、COC'分别为a、b、c边上的中线。根据重心性质可得OA'=1/3AA'、OB'=1/3BB'、OC'=1/3CC'。过O、A分别作a边上高OH'、AH，可得OH'=1/3AH，进而得到S△BOC=1/3S△ABC、S△AOC=1/3S△ABC、S△AOB=1/3S△ABC，因此S△BOC=S△AOC=S△AOB。

三角形内到三边距离之积最大的点。

证明：设点P是△ABC内的一点，连接PA、PB、PC，作点P到BC、AC、AB的垂线段，垂足分别为D、E、F，延长AP交BC于M。记△ABC的面积为S，BC为a，AC为b，AB为c，PD为a'，PE为b'，PF为c'。由已知条件可得aa'/2+bb'/2+cc'/2=S△BCP+S△ACP+S△ABP=S，因此aa'+bb'+cc'=2S。由均值不等式可得[(aa'+bb'+cc')/3]^3≥aa'bb'cc'=(abc)*(a'b'c')，当且仅当aa'=bb'=cc'时等号成立。因此a'b'c'≤[(aa'+bb'+cc')/3]^3/(abc)=(S/3)^3/(abc)=8S^3/(27abc)，当且仅当aa'=bb'=cc'时等号成立。所以a'b'c'只有当aa'=bb'=cc'时才会取得最大值。此时，S△ABP=cc'/2=bb'/2=S△ACP，由燕尾定理可得BM/CM=S△ABP/S△ACP=1。因此BM=CM，M是BC的中点，AM是△ABC的中线，P在△ABC中BC边的中线上。同理可证P在△ABC中AB、AC边的中线上。所以当a



声明：本站所有作品图文均由用户自行上传分享，仅供网友学习交流。若您的权利被侵害，请联系我们