高次三角函数积分公式及其应用

积分是微分的逆运算，通过求解导函数的原函数，我们可以得到函数的积分。在数学和应用领域，积分的作用广泛，它被用于求和、求曲边三角形的面积等。积分的性质包括线性性、保号性、极大值极小值、绝对连续性、绝对值积分等。

对于高次三角函数的积分，有一些基本和常用的积分公式。这些公式在解决复杂的积分问题时非常有用。

基本积分公式：这是积分的基础，包括对于常数、一次函数、二次函数等的积分。

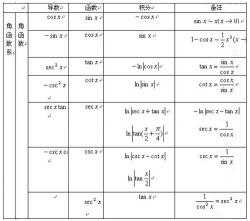
三角函数的有理式积分公式：对于形如 sin(nx)/cos(mx) 的三角函数有理式的积分，可以使用一些特定的公式进行求解。

这些高次三角函数积分公式在解决实际问题，如物理、工程、经济等领域的问题时非常有用。它们可以帮助我们理解和分析函数的性质，进一步揭示其内在规律。

在使用这些公式时，我们需要了解其适用的条件和范围，以确保结果的准确性和有效性。同时，对于一些复杂的积分问题，可能需要结合其他数学工具和方法进行求解。

高次三角函数的积分公式是数学领域的重要工具，它们的应用广泛且具有实际意义。