二次函数的顶点坐标公式及知识点

二次函数是数学中的基础知识之一，而其顶点坐标公式是理解二次函数性质的关键。下面我们将详细介绍二次函数的顶点坐标公式及其相关知识点。

一、二次函数的顶点坐标公式

二次函数的顶点坐标公式为：y = a(x - h)^2 + k，其中a、h、k为常数，且a≠0。这个公式表示二次函数的顶点坐标为(h, k)。

二、顶点坐标公式的推导过程

我们可以按照以下步骤推导二次函数的顶点坐标公式：

1、将二次函数的一般形式y = ax^2 + bx + c转化为顶点形式。这可以通过完全平方完成：

y = a(x^2 + bx/a + c/a)

2、进一步化简得到：

y = a(x^2 + bx/a + b^2/4a^2 + c/a - b^2/4a^2)

展开并整理得到：

y = a(x + b/2a)^2 + c - b^2/4a

3、我们可以得出顶点坐标为(-b/2a, (4ac - b^2)/4a)。

三、二次函数的其他表达式

一般式：y = ax^2 + bx + c，其中a、b、c为常数，a≠0，则称y为x的二次函数。其顶点坐标为(-b/2a, (4ac - b^2)/4a)。

交点式：函数图像与x轴交于和两点。其中a、b、c为常数，a≠0，且a决定函数的开口方向。

两根式：y = a(x - x1)(x - x2)，其中x1、x2是抛物线与x轴的交点的横坐标，即ax^2 + bx + c = 0的两个根，a=0。

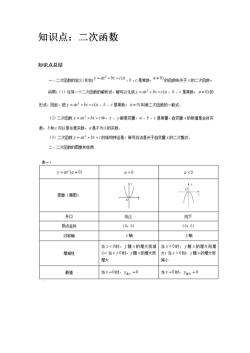
四、二次函数的性质

二次函数的图像是抛物线，但抛物线不一定是二次函数。开口向上或者向下的抛物线才是二次函数。抛物线是轴对称图形。对称轴为直线x=-b/2a。

二次项系数a决定抛物线的开口方向和大小。当a>0时，抛物线开口向上；当a<0时，抛物线开口向下。|a|越大，则抛物线的开口越小；|a|越小，则抛物线的开口越大。

一次项系数b和二次项系数a共同决定对称轴的位置。当a与b同号时（即ab>0），对称轴在y轴左侧；当a与b异号时（即ab<0），对称轴在y轴右侧。

通过以上介绍，我们可以看出二次函数的顶点坐标公式及其相关知识点在理解和应用二次函数中起着重要的作用。希望这些内容能够帮助你更好地理解和掌握二次函数的知识。