奇函数的性质探索

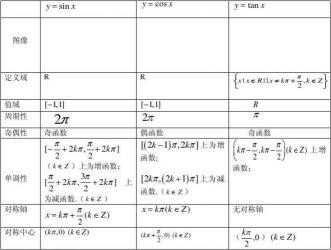
奇函数，作为数学中的一类重要函数，具有许多独特的性质。以下，我们将逐一探讨这些性质，并深入了解它们如何塑造函数的特性。

1、当两个奇函数进行相加或相减时，结果仍然是一个奇函数。这一性质表明，奇函数在加法或减法运算下是封闭的，保持了奇函数的特性。

2、一个偶函数与一个奇函数相加或相减时，得到的结果既不是奇函数也不是偶函数。这一性质揭示了奇函数与偶函数在运算中的互补性，它们相互结合可以产生新的、非标准的函数类型。

4、当两个奇函数相乘或相除时，得到的函数是偶函数。这一性质进一步强调了奇函数在乘法或除法运算下的特殊性，它们相乘或相除后转变为偶函数，呈现出与原始奇函数不同的性质。

3、一个偶函数与一个奇函数相乘或相除时，得到的函数是奇函数。这一性质揭示了奇函数与偶函数在运算中的另一种互补性，它们相乘或相除后保持了奇函数的特性，同时也体现了偶函数对结果的影响。

5、值得注意的是，只有当函数的定义域关于原点对称时，函数f(x)才能同时是奇函数和偶函数。这一性质强调了奇函数和偶函数在定义域上的对称性要求，为判断函数类型提供了重要依据。

奇函数具有多种独特的性质，在加法、减法、乘法、除法运算中表现出不同的特点。同时，奇函数与偶函数之间的运算关系也为我们提供了更多了解函数性质的视角。这些性质不仅在数学领域有着广泛的应用，也为我们理解和应用函数提供了有力的工具。